When Do Graph Neural Networks Help with Node Classification: Investigating the Homophily Principle on Node Distinguishability

Abstract

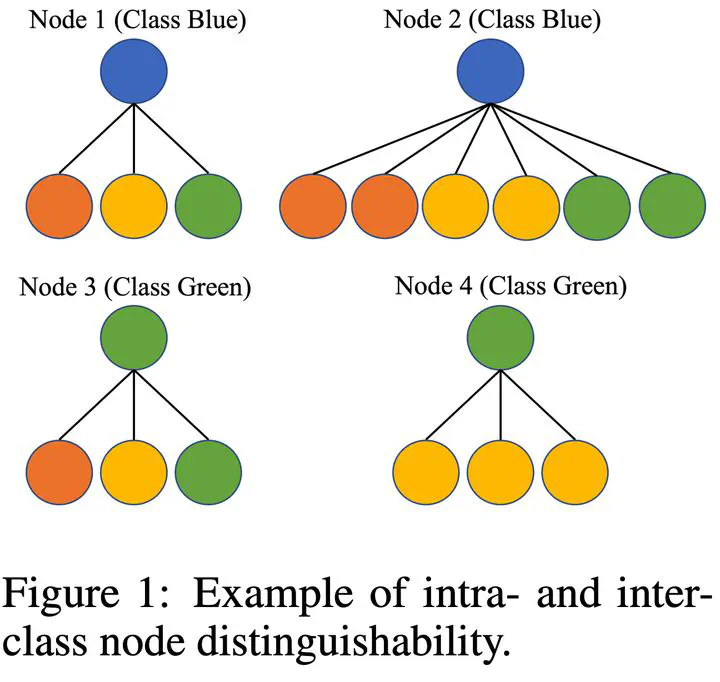
Homophily principle, i.e. nodes with the same labels are more likely to be connected, was believed to be the main reason for the performance superiority of Graph Neural Networks (GNNs) over Neural Networks (NNs) on Node Classification (NC) tasks. Recently, people have developed theoretical results arguing that, even though the homophily principle is broken, the advantage of GNNs can still hold as long as nodes from the same class share similar neighborhood patterns, which questions the validity of homophily. However, this argument only considers intra-class Node Distinguishability (ND) and ignores inter-class ND, which is insufficient to study the effect of homophily. In this paper, we first demonstrate the aforementioned insufficiency with examples and argue that an ideal situation for ND is to have smaller intra-class ND than inter-class ND. To formulate this idea and have a better understanding of homophily, we propose Contextual Stochastic Block Model for Homophily (CSBM-H) and define two metrics, Probabilistic Bayes Error (PBE) and Expected Negative KL-divergence (ENKL), to quantify ND, through which we can also find how intra- and inter-class ND influence ND together. We visualize the results and give detailed analysis. Through experiments, we verified that the superiority of GNNs is indeed closely related to both intra- and inter-class ND regardless of homophily levels, based on which we define Kernel Performance Metric (KPM). KPM is a new non-linear, feature-based metric, which is tested to be more effective than the existing homophily metrics on revealing the advantage and disadvantage of GNNs on synthetic and real-world datasets.