Bidirectional Learning for Offline Infinite-width Model-based Optimization
Abstract
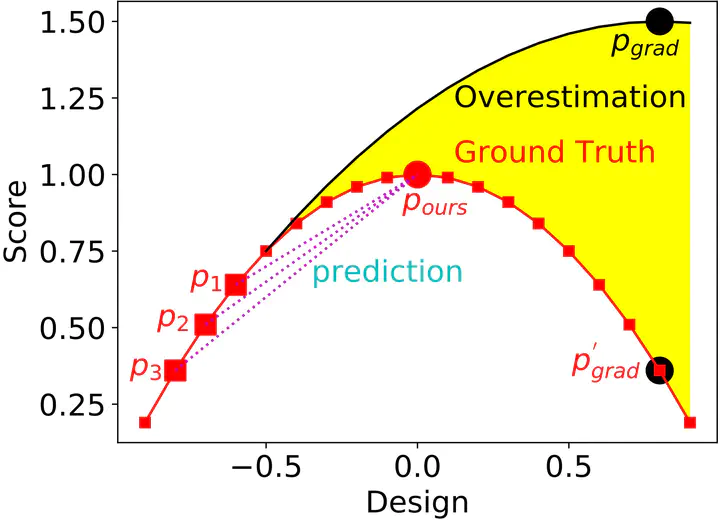
In offline model-based optimization, we strive to maximize a black-box objective function by only leveraging a static dataset of designs and their scores. This problem setting arises in numerous fields including the design of materials, robots, DNA sequences, and proteins. Recent approaches train a deep neural network (DNN) on the static dataset to act as a proxy function, and then perform gradient ascent on the existing designs to obtain potentially high-scoring designs. This methodology frequently suffers from the out-of-distribution problem where the proxy function often returns poor designs. To mitigate this problem, we propose BiDirectional learning for offline Infinite-width model-based optimization} (BDI). BDI consists of two mappings, the forward mapping leverages the static dataset to predict the scores of the high-scoring designs, and the backward mapping leverages the high-scoring designs to predict the scores of the static dataset. The backward mapping, neglected in previous work, can distill more information from the static dataset into the high-scoring designs, which effectively mitigates the out-of-distribution problem. For a finite-width DNN model, the loss function of the backward mapping is intractable and only has an approximate form, which leads to a significant deterioration of the design quality. We thus adopt an infinite-width DNN model, and propose to employ the corresponding neural tangent kernel to yield a closed-form loss for more accurate design updates. Experiments on {various} tasks verify the effectiveness of BDI.