Large Language Model and Beyond
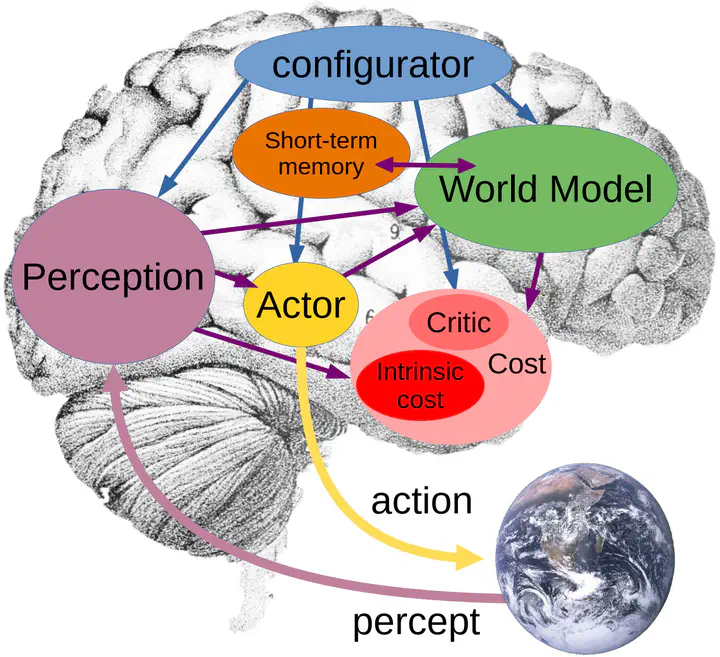Taken from “A Path Towards Autonomous Machine Intelligence”, by Yann LeCun
Existing Works
Neural Architectures
- HyperMoE: Towards Better Mixture of Experts via Transferring Among Experts, arXiv 2024.2
- Empirical Study on Updating Key-Value Memories in Transformer Feed-forward Layers, arXiv 2024.2
- Prototype-based HyperAdapter for Sample-Efficient Multi-task Tuning, EMNLP 2023
- Beyond Fully-Connected Layers with Quaternions: Parameterization of Hypercomplex Multiplications with $1/n$ Parameters, ICLR 2021
Data & Benchmark
- CMMMU: A Chinese Massive Multi-discipline Multimodal Understanding Benchmark, arXiv 2024.1
- MARBLE: Music Audio Representation Benchmark for Universal Evaluation, NeurIPS 2023
- Chinese Open Instruction Generalist: A Preliminary Release, arXiv 2023
Multi-Modal & Reinforcement Learning
- Read to Play (R2-Play): Decision Transformer with Multimodal Game Instruction, arXiv 2024.2
- MERT: Acoustic Music Understanding Model with Large-Scale Self-supervised Training, ICLR 2024
- Think Before You Act: Decision Transformers with Internal Working Memory, arXiv 2023
- Interactive Natural Language Processing, arXiv 2023
Human-AI Alignment
- AI Alignment: A Comprehensive Survey, arXiv 2023
- Would you Rather? A New Benchmark for Learning Machine Alignment with Cultural Values and Social Preferences, ACL 2020
Next
- Truly modular LLMs
- LLMs with lifelong learning
- Tight human alignment
Jie Fu
Visiting Scholar
Focus on Deep Learning, Language Processing, Human-AI Alignment, Multi-Modal Learning.